امید ریاضی - گشتاور مرتبه‌ی nام

در این مطلب بصورت خلاصه با مثال‌های کاربردی به شرح امید ریاضی - ممان مرتبه‌ی nام و کاربرد آنها خواهیم پرداخت.

امید ریاضی

برابر با حد متوسط یا به عبارتی میانگینی از احتمال رخ دادن یک متغیر تصادفی است.

$$E(X)=\sum _{i=1}^n{x}_{i}P(x_i)$$

گشتاورها یا Moments

شاخص‌هایی هستند که خصوصیات توابع توزیع احتمال یا PDF ها را توصیف می‌کنند. فرمول زیر فرمول کلی محاسبه‌ی گشتاور kام است.

$${\mu }_n=E(X-\mu {)}^k=\sum _{i=1}^n(x_i-\mu {)}^{k}P(x_i)$$

گشتاور صفرم برای یک متغیر تصادفی، برابر با کل احتمال یا مقدار ۱ است. گشتاور اول بیانگر میانگین و گشتاور مرکزی دوم نیز واریانس (Variance) را مشخص می‌کند. گشتاورهای سوم و چهارم نیز متناسب با چولگی و کشیدگی توزیع احتمال متغیر تصادفی خواهند بود.

گشتاور اول: میانگین
Mean: 1st Raw Moment

$$E(X)=\sum _{i=1}^n{x}_{i}P(x_i)$$

گشتاور دوم: واریانس یا پراکندگی
Variance: 2nd Central Moment

$$variance={\sigma }^2=E(X-\mu {)}^2=\sum _{i=1}^n(x_i-\mu {)}^{2}P(x_i)$$

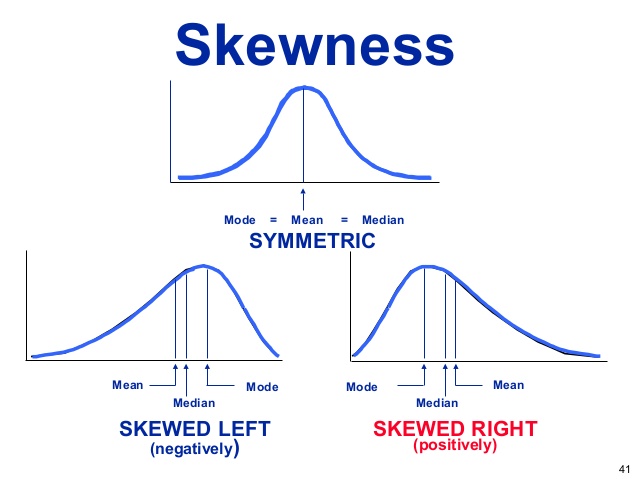
گشتاور سوم استاندارد شده: چولگی
Skewness: Standradized 3nd Central Moment

$$skewness=\frac{E(X-\mu {)}^3}{{\sigma }^3}=\frac{{\sum }_{i=1}^n(x_i-\mu {)}^{3}P(x_i)}{{\sigma }^3}$$

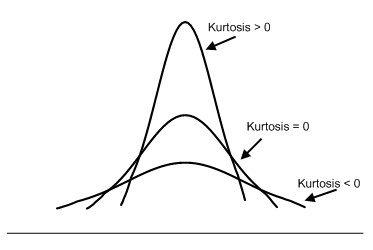
گشتاور چهارم استاندارد شده: کشیدگی
Kurtosis: Standardized 4nd Central Moment

$$skewness=\frac{E(X-\mu {)}^4}{{\sigma }^4}=\frac{{\sum }_{i=1}^n(x_i-\mu {)}^{4}P(x_i)}{{\sigma }^4}$$