داده کاوی - ۴ - معیار‌های فاصله

۲۴ فروردین ۱۳۹۹

فاصله‌ها و شباهت‌ها

فاصله‌ها و شباهت‌های اشیاء که با مقایسه ویژگی‌های آنها بدست می‌آید از دسته شاخص‌های پرکاربرد در روش‌های مختلف داده کاوی هستن. معیار فاصله با معیار شباهت رابطه عکس دارد بطوریکه هر چه فاصله بیشتر باشد آن‌ها از هم دورتر بوده و شباهت آنها کمتر است و برعکس.  

شرح یک مسئله

فرض کنید می‌خواهیم میزان فاصله یا شباهت سلیقه افراد در فیلم‌ها را با داشتن امتیازاتی که برای آنها ثبت کردن محاسبه کنیم. برای این منظور می‌توانیم از روش‌های محاسبه فاصله‌ها و شباهت‌هایی که در حوزه‌ی داده‌کاوی مطرح است استفاده‌کنیم. یاد‌آوری: همانطور که در قسمت جزئیات دیتاست‌ها گفته شد، دیتاست مورد استفاده movie_rating_simple بصورت زیر است.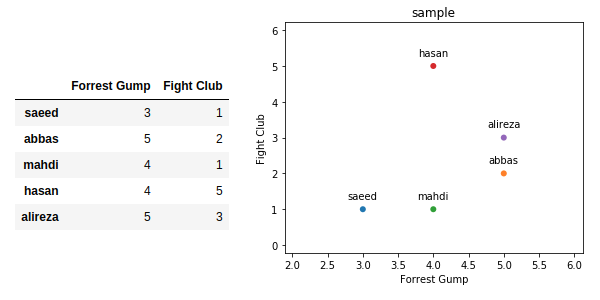
 movieratings_simple.json

فاصله‌ها

در این قسمت به شرح انواع «معیار‌های فاصله» یا Distance Metrics که برای محاسبه فاصله دو شیئ یا به عبارتی میزان دور بودن آنها استفاده می‌شود، بپردازیم. شرایط معیارهای فاصله
۱ـ اندازه فاصله همیشه نامنفی است.
۲ـ اگر فاصله‌ی بین دو نقطه صفر باشد آن دو نقطه یکی هستن و بر عکس.
۳ـ در صورت جابجایی مبدا و مقصد بین دو نقطه‌ی ثابت فاصله‌ها به یک اندازه باشند. F(a,b)=F(b,a)F(a,b) = F(b,a) ۴ـ نامساوی مثلثی، صادق باشد مطابق شکل زیر برای هر سه نقطه‌ی دلخواه
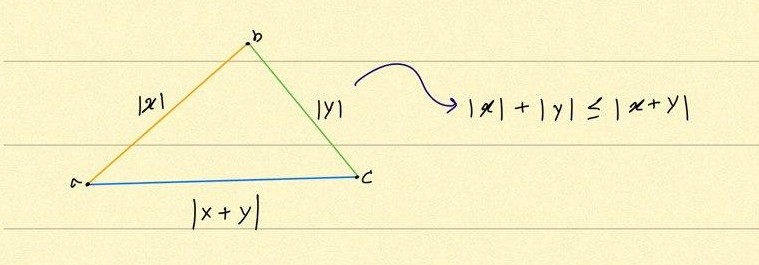
*یادآوری: نامساوی مثلثی بیان می‌کند مجموع دو طول یک مثلث بزرگتر از ضلع سوم آن است.

 

فاصله اقلیدسی

فاصله‌ی اقلیدسی مانند قضیه فیثاغورس برابر است با ریشه دوم مجموع مربعات اختلاف ویژگی‌های اشیاء \fq,p=(q1−p1)2+⋯+(qn−pn)2=∑i=1n(qi−pi)2\f{q,p} = \sqrt{(q_1-p_1)^2+\cdots+(q_n-p_n)^2}\\= \sqrt{\sum_{i=1}^{n}(q_i-p_i)^2} به مثال زیر که در ادامه برای فاصله‌های دیگر نیز بررسی می‌کنیم دقت کنید.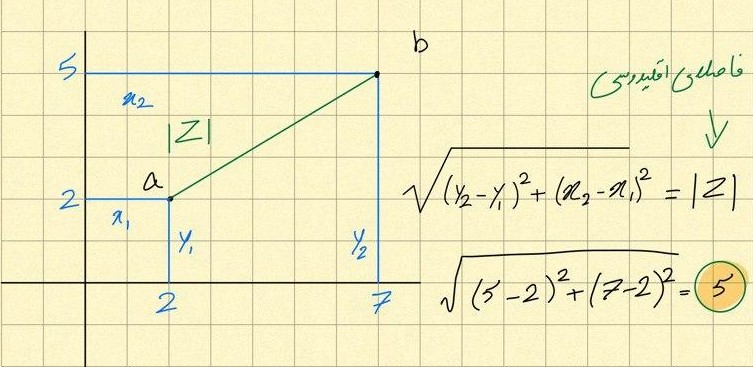
 

 پیاده‌سازی روش اقلیدسی در پایتون

def get_euclidean_distance(rating1,rating2):
    distance = 0
    for key in rating1:
        if key in rating2:
            distance += pow(abs(rating1[key]-rating2[key]), 2)
    return pow(distance, 1/2)
 
dt=movie_rating_simple_dict
 
print('abbas-hasan:%f'%+get_euclidean_distance(dt['abbas'],dt['hasan']))
print('abbas-alireza:%f'%get_euclidean_distance(dt['abbas'],dt['alireza']))
print('abbas-mahdi:%f'%+get_euclidean_distance(dt['abbas'],dt['mahdi']))
print('abbas-saeed:%f'%+get_euclidean_distance(dt['abbas'],dt['saeed']))
 
// result ---------------
// abbas-hasan:3.162278
// abbas-alireza:1.000000
// abbas-mahdi:1.414214
// abbas-saeed:2.236068

فاصله منهتن یا فاصله‌ی راننده تاکسی

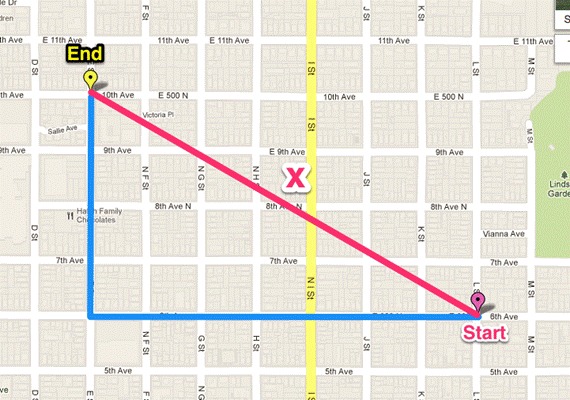
illustrativemathematics خط آبی نشان دهنده‌ی فاصله‌ی راننده‌ تاکسی یا منهتن، بین دو نقطه‌ی Start و End است و خط قرمز نشان دهنده‌ی فاصله‌ی اقلیدوسی می‌باشد. فاصله‌ی منهتن ساده‌ترین معیار برای محاسبه‌ی فاصله است که برابر است با مجموع قدر مطلق اختلاف ویژگی‌های اشیاء.

 

محاسبه‌ی فاصله به روش منهتن

 

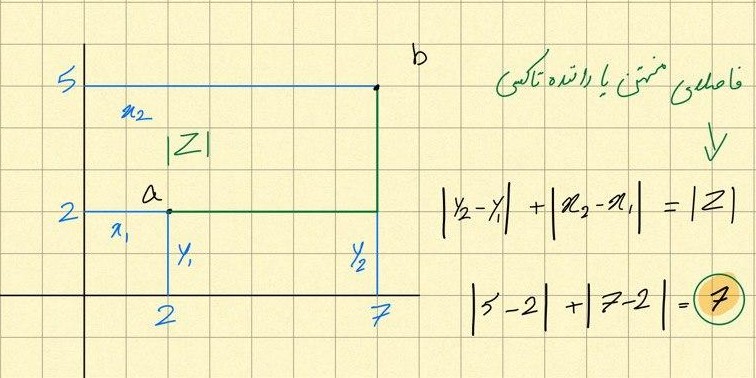
پیاده‌سازی روش منهتن در پایتون

def get_manhattan_distance(rating1,rating2):
    distance = 0
    for key in rating1:
        if key in rating2:
            distance += abs(rating1[key] - rating2[key])
    return distance
 
dt=movie_rating_simple_dict
 
print('abbas-hasan:%s'%+get_manhattan_distance(dt['abbas'],dt['hasan']))
print('abbas-alireza:%s'%get_manhattan_distance(dt['abbas'],dt['alireza']))
print('abbas-mahdi:%s'%+get_manhattan_distance(dt['abbas'],dt['mahdi']))
print('abbas-saeed:%s'%+get_manhattan_distance(dt['abbas'],dt['saeed']))
 
// result ------------------
// abbas-hasan:4
// abbas-alireza:1
// abbas-mahdi:2
// abbas-saeed:3
 

فاصله چبیشف

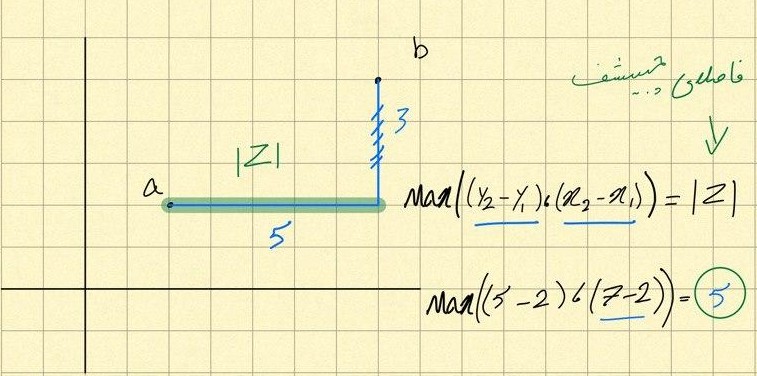
یا به عبارتی دیگر فاصله‌ی چبیشف برابر است با حداکثر اختلافی که بین ویژگی‌های اشیاء وجود دارد.

محاسبه‌ی فاصله به روش چبیشف

 

پیاده‌سازی روش چبیشف در پایتون

def get_chebychev_distance(rating1,rating2):
    distance = 0
    for key in rating1:
        if key in rating2:
            candidate_distance = abs(rating1[key] - rating2[key])
            if(candidate_distance>distance):
                distance = candidate_distance            
    return distance
 
dt=movie_rating_simple_dict
 
print('abbas-hasan:%s'%+get_chebychev_distance(dt['abbas'],dt['hasan']))
print('abbas-alireza:%s'%get_chebychev_distance(dt['abbas'],dt['alireza']))
print('abbas-mahdi:%s'%+get_chebychev_distance(dt['abbas'],dt['mahdi']))
print('abbas-saeed:%s'%+get_chebychev_distance(dt['abbas'],dt['saeed']))
 
// result ---------------
// abbas-hasan:3
// abbas-alireza:1
// abbas-mahdi:1
// abbas-saeed:2

فاصله مینکوفسکی

یک معیار کلی و تعمیم یافته است، به این معنا که می‌توان با تغییر فرمول فاصله‌های متفاوتی را محاسبه کرد. (∑i=1n∣xi−yi∣p)1/p({\sum_{i=1}^{n}{\left | x_i-y_i \right | }^p})^{^1/_p} برای مثال با تغییر مقدار p در معادله‌ی فوق به سه فاصله‌ی متفاوت زیر می‌رسیم. اگر بجای p عدد ۱ را قرار دهیم، تبدیل به فاصله‌ی منهتن می‌شود. اگر بجای p عدد ۲ را قرار دهیم، تبدیل به فاصله‌ی اقلیدسی می‌شود. اگر بجای p عدد ∞ (یا بینهایت) را قرار دهیم، تبدیل به فاصله‌ی چبیشف می‌شود. ** نکته: هر چه p بزرگتر باشد، میزان تاثیر اختلاف زیاد در یک ویژگی روی نتیجه بیشتر خواهد شد.

پیاده‌سازی روش مینکوفسکی در پایتون

def get_minkowski_distance(rating1, rating2, q):
    distance = 0
    commonRatings = False
    for key in rating1:
        if key in rating2:
            distance += pow(abs(rating1[key]-rating2[key]), q)
            commonRatings = True
    if(commonRatings):
        return pow(distance, 1/q)
    else:
        return 0
        
dt=movie_rating_simple_dict
 
print('q=1 abbas-hasan:%f'%get_minkowski_distance(dt['abbas'],dt['hasan'],1))
print('q=2 abbas-hasan:%f'%+get_minkowski_distance(dt['abbas'],dt['hasan'],2))
print('q=3 abbas-hasan:%f'%+get_minkowski_distance(dt['abbas'],dt['hasan'],300))
 
// result -------------------------
// q=1 abbas-hasan:4.000000
// q=2 abbas-hasan:3.162278
// q=3 abbas-hasan:3.000000
لینک مخزن گیت‌هاب کدهای این مطلب

فهرست مطالب « داده کاوی در پایتون »

Berneti