داده کاوی - ۶ - ضریب همبستگی پیرسون

۳۱ فروردین ۱۳۹۹

مسئله

فرض کنید در مجموعه‌ی داده‌های ratings_grade_inflation.json که در

#داده کاوی - ۳ - جزئیات دیتاست‌ها

به شرح جزئیات آن پرداختیم، می‌خواهیم میزان شباهت بین افراد را محاسبه کنیم.

Namem1m2m3m4
Saeed3.01.04.02.00
Abbas2.03.03.04.00
Alireza4.54.05.04.25

با اولین نگاه به امتیازات alireza متوجه می‌شود که بازه‌ی امتیازات او در محدوده‌ ۴ تا ۵ است (تنوع درجه و یا grade inflation) و اگر بخواهیم صرفا با مشاهدات خود میزان شباهت را حدس بزنیم می‌توانیم بگوییم شباهت saeed-alireza بیشتر از saeed-abbas است زیرا امتیازاتی که alireza ثبت کرده‌است با امتیازات سعید متناسب است، برای مثال کمترین امتیاز alireza که برابر ۴ برای فیلم m2 بوده متانسب است با کمترین امتیاز saeed که برای همین فیلم m2 با امتیاز ۱ است ویا امتیاز حداکثر علیرضا که ۵ بوده برای فیلم m3 برابر حداکثر امتیاز سعید برای همان فیلم با امتیاز ۴ است. درصورتی که تناسب امتیازات saeed و عباس تقریبا برخلاف هم است و در نتیجه انتظار داریم شباهت saeed-alireza بیشتر از saeed-abbas باشد.

حال بگذارید امتیازهای saeed-alireza و saeed-abbas را با استفاده از نمودار مقایسه کنیم.

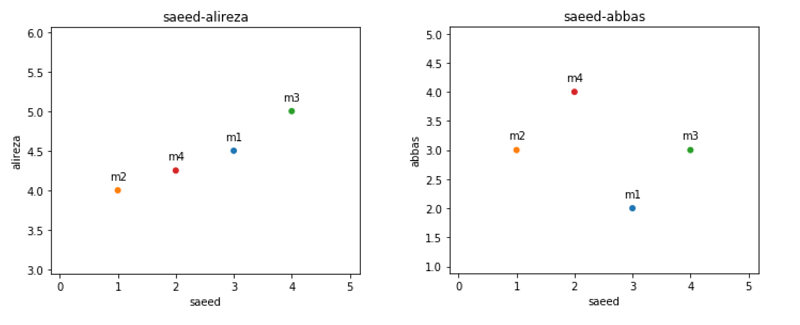
نمودار مقایسه داده‌ها | ضریب همبستگی پیرسون

همانطور که مشاهده می‌کنید نمودار امتیازات saeed-alireza در راستای یک خط مستقیم هست و نمودار امتیازات saeed-abbas بصورت پراکنده است.


نکته مهمی که باقیمیماند این است که صرفا در راستای یک خط راست بودن نشان دهنده‌ی تفاهم کامل نیست زیرا اگر این خط بر خلاف نمودار saeed-alireza بصورت نزولی باشد نشان دهنده‌ی عدم تفاهم کامل است.

یکی از راهکارهایی که می‌تواند با توجه به داده‌های ورودی ما و خروجی مدنظر ما را تولید کند استفاده از ضریب همبستگی پیرسون است که رفتاری مشابه آنچه که ما می‌خواهیم با توجه به نوع پراکندگی نقاط دارد.

ضریب همبستگی پیرسون یا pearson correlation coefficient

ضریب همبستگی پیرسون برای دو متغیر عددی در بازه‌ی ۱ تا ۱- است که ۱ به معنای تفاهم کامل و ۱- نشانه‌ی عدم تفاهم کامل است.


در نمودارهای زیر مشاهده می‌کنید که حاصل محاسبه‌ی ضریب همبستگی پیرسون روی متغیرهای مختلف چقدر به رفتار مد نظر ما نزدیک است.

www.mathsisfun.com

برای مثال ضریب همبستگی داده‌هایی که روی یک خط مستقیم و صعودی قرار گرفته‌اند عدد یک به دست آمد که به معنای شباهت کامل برای ما تلقی می‌شد.

فرمول ضریب همبستگی پیرسون r=∑i=1n(xi−xˉ)(yi−yˉ)∑i=1n(xi−xˉ)2∑i=1n(yi−yˉ)2xˉ=1n∑i=1nxi∗yˉ=1n∑i=1nyir = \frac {\sum_{i=1}^{n}{(x_i-\bar{x})(y_i-\bar{y}})} {\sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^n(y_i-\bar{y})^2}} \\\footnotesize{ {\bar{x}=\frac{1}{n}\sum_{i=1}^{n}{x_i}} \enspace * \enspace {\bar{y}=\frac{1}{n}\sum_{i=1}^{n}{y_i}} }

برای پیاده‌سازی الگوریتم فرمول بالا نیاز هست تا چند بار از روی تمام داده‌ها بگذریم و که اسطلاحا به آن multipass می‌گویند.

فرمول ضریب همبستگی پیرسون اصلاح شده

فرمول زیر تقریبی از فرمول اصلی محاسبه‌ی ضریب همبستگی پیرسون است که مسئله‌ی multipass بودن الگوریتم را حل می‌کند و به اصطلاح singlepass است و در نتیجه پیچیدگی کمتری دارد و سرعت اجرای آن بالاتر است.

r=∑i=1nxiyi−∑i=1nxi∑i=1nyin∑i=1nxi2−(∑i=1nxi)2n∑i=1nyi2−(∑i=1nyi)2nr = \frac { \sum_{i=1}^{n}{x_i y_i} -\frac{\sum_{i=1}^{n}x_i\sum_{i=1}^{n}y_i}{n} } { \sqrt{ \sum_{i=1}^{n}x_i^2-\frac{{(\sum_{i=1}^{n}x_i)}^2}{n} } \sqrt{ \sum_{i=1}^{n}y_i^2-\frac{{(\sum_{i=1}^{n}y_i)}^2}{n} } }

پیاده‌سازی ضریب همبستگی پیرسون اصلاح شده در پایتون

متد pearson دو لیست از اعداد مرتبط با دو متغیر را گرفته و ضریب همبستگی آنها را محاسبه و بر می‌گرداند.

def pearson(rating1, rating2):
    sum_xy = 0
    sum_x = 0
    sum_y = 0
    sum_x2 = 0
    sum_y2 = 0
    n = 0
    for key in rating1:
        if key in rating2:
            n += 1
            x = rating1[key]
            y = rating2[key]
            sum_xy += x * y
            sum_x += x
            sum_y += y
            sum_x2 += pow(x, 2)
            sum_y2 += pow(y, 2)
    
    denominator = sqrt(sum_x2 - pow(sum_x, 2) / n) * sqrt(sum_y2 - pow(sum_y, 2) / n)
    if denominator == 0:
        return 0
    else:
        return (sum_xy - (sum_x * sum_y) / n) / denominator

نتیجه محاسبه ضریب همبستگی پیرسون برای saeed-alireza و saeed-abbas بصورت زیر است.

saeed-alireza:0.982708
saeed-abbas:-0.316228

همانطور که پیشبینی می‌کردیم ضریب همبستگی پیرسون که به عنوان معیاری برای میزان شباهت در نظر گرفتیم برای saeed-alireza بیشتر از saeed-abbas است.

حال می‌خواهیم بررسی کنیم آیا با استفاده از فاصله منهتن نیز که در

/داده کاوی - ۴ - معیار‌های فاصله

شرح داده شده به نتایج مورد انتظار می‌رسیم یا خیر.


نکته‌ای که نیاز به یادآوری دارد این است که مفهوم فاصله با شباهت رابطه عکس دارد و فاصله‌ی کمتر بیانگر شباهت بیشتر است و در نتیجه با توجه به موارد گفته شده ما انتظار داریم فاصله‌ی saeed-alireza کمتر از saeed-abbas باشد.


خروجی زیر نتایج محاسبه‌ی فاصله‌ی منهتن می‌باشد.

saeed-alireza:7.750000
saeed-abbas:6.000000

اما نتایج بدست آمد برخلاف انتظار ما بدست آمد و مشکل از آنجاییست که که در فاصله‌ی منهتن تنوع در امتیازدهی که اصطلاحا تنوع درجه و یا grade inflation در نظر گرفته نمی‌شود و این به این معناست تشابه امتیازدهی alireza به saeed با توجه به اینکه او تنها در بازه‌ی ۴ تا ۵ امتیازدهی کرده در نظر گرفته نمی‌شود.

فهرست مطالب « داده کاوی در پایتون »

Berneti