داده کاوی - ۵ - شباهت کسینوسی

معیارهای شباهت

معیارهای شباهت، معیارهایی مانند معیارهای فاصله هستند که میزان دور و یا نزدیک بودن دو موجودیت را مشخص می‌کنند. بدیهی است که معیار شباهت با معیارهای فاصله رابطه عکس دارند و به عبارتی هر چه میزان شباهت بیشتر باشد می‌توان نتیجه گرفت فاصله‌ی دو شیئ کمتر است.

در این بخش به شرح چند معیار شباهت و شیوه‌ی پیاده‌سازی آنها در پایتون خواهیم پرداخت.

شباهت کسینوسی یا Cosine similarity

شباهت کسینوسی یک معیار شباهت است که پایه آن محاسبه‌ی میزان کسینوس زاویه‌ی بین دو بردار است.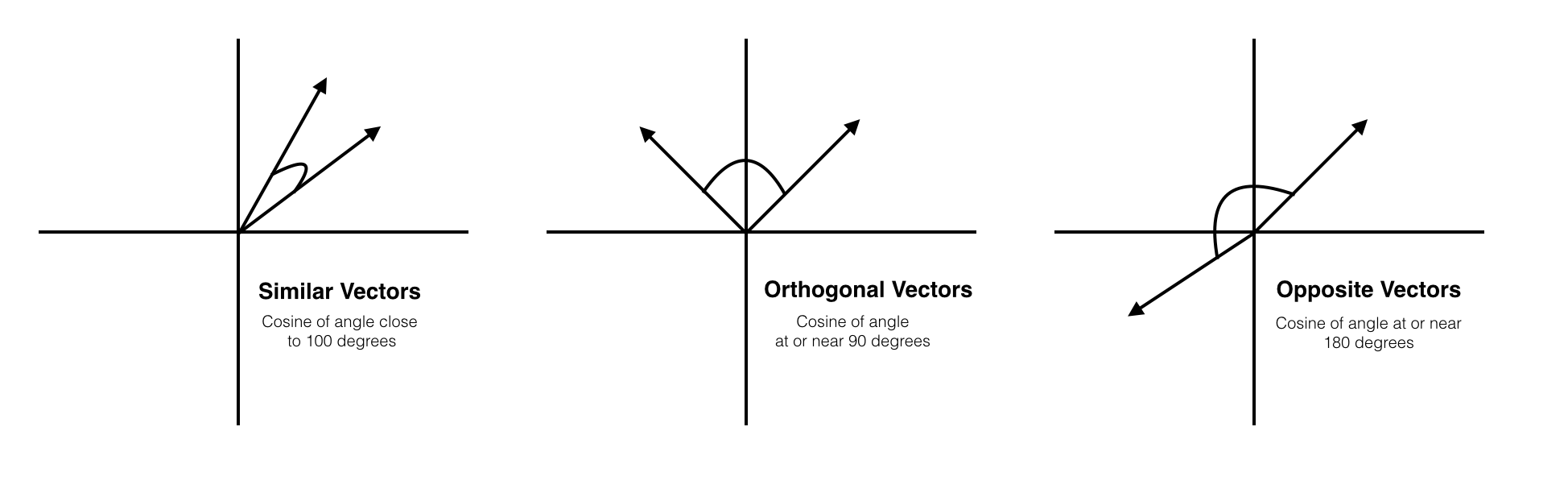

در صورت انطباق دو بردار (در این معیار نشانه شباهت کامل است) که زاویه‌ی بین دو بردار صفر می‌باشد مقدار آن برابر ۱ خواهد شد و در کمترین میزان شباهت دو بردار یعنی اگر زاویه بین دو بردار ۱۸۰ درجه باشد نتیجه این معیار ۱- خواهد شد.

$$cos(x,y)=\frac{x\cdot y}{||x||\cdot ||y||}=\frac{{\sum }_{i=1}^n{x}_i{y}_i}{\sqrt{{\sum }_{i=1}^n(x_i{)}^2}\sqrt{{\sum }_{i=1}^n(y_i{)}^2}}$$

این معیار یکی از پرکاربردترین معیارها در پردازش متن است. معیار شباهت کسیونوسی برای استفاده در زمانیکه داده‌های مربوط به ویژگی‌های ما تنک یا sparse هستن مناسب است.

داده‌های تنک یا sparse

برای شرح داده‌های تنک یا اسپارس از یک مثال استفاده می‌کنیم. 
فرض کنیم می‌خواهیم میزان شباهت دو کتاب انگلیسی را محاسبه کنیم. کلمات یکتای زبان انگلیسی که حدود یک میلیون واژه است می‌تواند ویژگی‌های ما باشد و تعداد تکرار هر کلمه در آن کتاب مقادیر آن ویژگی‌ها. آن دو کتاب می‌تواند کتاب 'عقل و احساس' با حدود ۷ هزار کلمه و کتاب 'هری پاتر و سنگ جادو' با حدود ۶ هزار کلمه‌ی یکتا باشد بدیهی است که حجم بسیار زیادی از ویژگی‌های ما که تعداد کلمات منحصربفرد زبان انگلیسی است خالی مانده و یا به عبارتی مقدار صفر می‌گیرند که در چنین شرایطی می‌گوییم داده‌های ویژگی‌های مسئله تنک است.
در نقطه مقابل مفهوم تنک اگر تمام ویژگی‌ها یا اکثر آنها دارای مقدار باشند می‌گوییم داده‌های مسئله غلیظ است.

ویژگی‌های شباهت کسینوسی

۱ـ شباهت کسینوسی به ضرایب مختلف ویژگی‌ها توجه نمی‌کند.
برای مثال فرض کنید فردی به فیلم‌های m1 و m2 حداقل امتیاز را با مقدار یک ثبت کرده و دیگری برای آن دو فیلم حداکثر امتیاز را با مقدار ۵ ثبت کرده‌است، در این شرایط شباهت کسینوسی این دو فرد برابر یک می‌شود که نشانه شباهت کامل در این معیار است.

۲ـ این معیار مقادیر صفر برای ویژگی‌ها را در نظر نمی‌گیرد.
یعنی مناسب زمانیست که صفر به معنای خالی و نامشخص بودن حالت ویژگی در مسئله باشد. مثلا اگر دو مقدار صفر نشان دهنده‌ی ثبت نشدن امتیاز دو فرد برای یک محصول باشد می‌توان از این معیار استفاده نمود، ولی اگر نشان دهنده‌ی امتیاز پایین آن دو شخص باشد که در این حالت می‌توان نتیجه گرفت که نظر این دو فرد مشابه است این معیار به خوبی عمل نمی‌کند زیرا این حالت را در نظر نمی‌گیرد. در چنین شرایطی جابجایی بازه‌ی امتیازات برای مثال بجای ۰ تا ۵ به یک تا ۶ می‌تواند یکی از راه کارهای مفید باشد تا بتوان از این معیار شباهت کسینوسی استفاده نمود.

شرح مسئله

فرض کنید می‌خواهیم با استفاده از مجموعه داده‌های ratings_sparseness.json که در #داده کاوی - ۳ - جزئیات دیتاست‌ها ساختار آن شرح داده شد میزان تشابه دو فرد را با استفاده از معیار شباهت کسینوسی محاسبه کنیم و جواب‌های بدست آمده را با میزان فاصله آنها با معیار‌ اقلیدوسی که در قسمت #داده کاوی - ۴ - معیار‌های فاصله به شرح آن پرداختیم مقایسه کنیم.

با مشاهده‌ی جدول زیر می‌توان به این نتیجه رسید که شباهت saeed و alireza بیشتر تر از شباهت saeed و abbas می‌باشد و اگر بخواهیم از دیدگاه فاصله نگاه کنیم فاصله‌ی بین امتیازات saeed و alireza کمتر از saeed و abbas است.

پیاده‌سازی شباهت کسینوسی در پایتون

ابتدا تابعی برای محاسبه‌ی ضرب داخلی که ورودی آن دو لیست از اعداد هست را به نام dot بصورت زیر پیاده‌سازی می‌کنیم.
سپس تابع cosine_similarity که لیست امتیازهای دو فرد را گرفته و طبق فرمول ذکر شده شباهت کسینوسی را محاسبه می‌کند را پیاده‌سازی می‌کنیم. در دو خط ابتدایی این تابع ابتدا مقادیر خالی که در اینجا مقدار '-' دارند را از لیست ورودی‌ها و سپس محاسبات را انجام می‌دهیم. 

def dot(A,B): 
    return (sum(a*b for a,b in zip(A,B)))

def cosine_similarity(rating1,rating2):
    rating1 = dict(filter(lambda x: x[1] != '-', rating1.items()))
    rating2 = dict(filter(lambda x: x[1] != '-', rating2.items()))
    a = rating1.values()
    b = rating2.values()
    return dot(a,b) / ( (dot(a,a) **.5) * (dot(b,b) ** .5) )

نتیجه بصورت زیر است:

saeed-alireza:0.801784
saeed-abbas:0.559893

همانطور که مشاهده می‌کنید نتایج بدست آماده با نظر ما مطابقت داشته حال بیاید بیبینم که آیا فاصله‌ها که باید بر خلاف میزان شباهت برای saeed و alireza کمتر از saeed و abbas باشد نیز درست بدست می‌آید؟!

ما در داده کاوی - ۴ - معیار‌های فاصله به شرح پیاده‌سازی معیارهای فاصله پرداختیم و در اینجا صرفا نتایج استفاده از آن توابع را ذکر می‌کنیم.

// manhattan_distance
saeed-alireza:2.000000
saeed-abbas:2.000000

//euclidean_distance
saeed-alireza:1.414214
saeed-abbas:1.414214

همانطور که مشاهده می‌کنید نتایج بدست آمده از معیارهای فاصله در این مسئله برخلاف نظر ماست زیرا میزان شباهت افراد و امتیازات یکسان هیچ تاثیری بر نتیجه آن نگذاشته‌است و میزان فاصله افراد با هر دو معیار اقلیدوسی و منهتن برای saeed-alireza و saeed-abbas یکسان بدست آمد.

• لینک مشاهده‌ی کدها و نتیجه‌ی اجرا
• لینک کدهای این قسمت در گیت هاب

در آموزش بعدی به شرح /داده کاوی - ۶ - ضریب همبستگی پیرسون که یکی از معیارهای محاسبه‌ی شباهت است خواهیم پرداخت