شاخصهای تمرکز
۱ـ میانگین (Mean)برای مطالعهی بیشتر در رابطه با انواع میانگینها به
انواع روشهای محاسبهی میانگین (میانگینهای فیثاغورثی)
مراجعه کنید.
۲ـ میانه (Median)برای محاسبهی میانه ابتدا دادهها را بصورت صعودی مرتب میکنیم، اگر تعداد دادهها فرد باشد عدد وسط را به عنوان میانه در نظر میگیریم و اگر زوج باشد میانه برابر میانگین دو دادهی وسط یعنی نصف مجموع آن دو میباشد.
نکته: مزیت این شاخص نسبت به میانگین این است که دادههای پرت در نتیجه هیچ تاثیری ندارند.
۳ـ مد یا نما (Mode)برای محاسبهی نما ابتدا فراوانی دادهها را پیدا میکنیم آن دادهای که فراوانیاش بیشتر بودهاست را به عنوان نما در نظر میگیریم. اگر دو دادهی غیر مجاور دارای فراوانی یکسان و بیش از سایر فراوانیها باشند، هر دو را به عنوان نما در نظر میگیریم و اگر آن دو در مجاورت هم باشد نصف مجموع آنها را به عنوان نما در نظر میگیریم و اگر فراوانی همهی دادهها یکسان باش میگوییم که دادهها بدون نما هستند. به مثالهای زیر توجه کنید.
برای دادههای 2,8,3,7,3,9,3,7,9,3,7 نما برابر 3 است چون فراوانی دادهی 3 از همه بیشتر است.
برای دادههای 5,6,7,3,7,9,6,5,7,5 چون فراوانی دو دادهی غیر مجاور 3 و 5 از سایر دادهها بیشتر است پس دادهها دو نمایی هستن که یکی برابر 3 و دیگر برابر 5 است.
برای دادههای 3,8,2,5,3,6,5,8,3,2,5 چون چون فراوانی دو دادهی مجاورر 3 و 5 یکسان است پس نما برابر نصف حاصل جمع آن دو یعنی 4 است.
برای دادههای 3,6,7,4,7,6,3,4 چون فراوانی همهی دادهها یکسان است پس دادهها بدون نما هستن.
به تصویر زیر توجه کنید، با مقایسهی مقادیر این سه شاخص تمرکز میتوانید مشخص کنید یک نمودار متقارن است یا دارای چولگی (Skewness) به چپ و راست است.
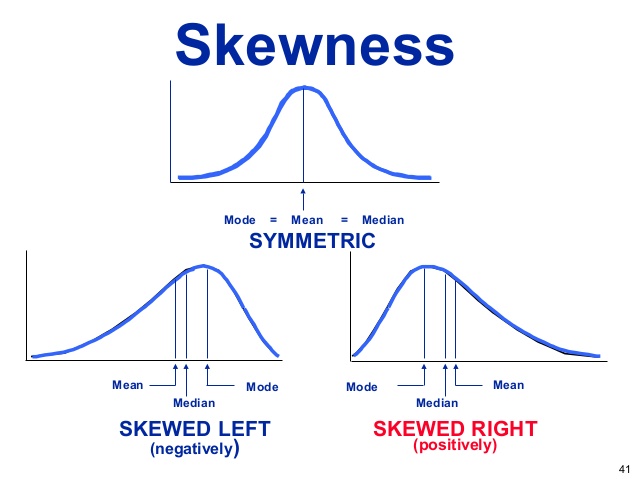
شاخصهای پراکندگی
۱ـ دامنهی دادهها برابر اختلاف بزرگترین و کوچکترین دادهاست. ۲ـ میانگین انحرافات به میانگین اختلافات هر داده از میانگین، میانگین انحرافات میگویند. ۳ـ واریانس و انحراف استاندارد با میانگین مجذور انحرافات، واریانس مینامند.به جذر انحراف استاندارد انحراف معیار میگویند.
۴ـ ضریب تغییر یا CVواریانس و انحراف استاندارد به واحد اندازه گیری دادهها بستگی دارند. برای مقایسه دو سری داده بایستی از شاخصهایی استفاده کنیم که به واحد اندازه گیری دادهها بستگی نداشته باشند. یکی از این شاخصها ضریب تغییر است:
که معمولا بصورت درصد بیان میشود.
مثال: کارخانهای دو نوع لامپ تولید میکند. لامپ نوع اول دارای میانگین طول عمر ۲۰۰ ساعت با انحراف استاندارد ۱۱ ساعت و لامپ نوع دوم دارای میانگین طول عمر ۲۴۰ ساعت با انحراف استاندارد ۱۲ ساعت است. کدام لامپ بهتر است؟
بنابراین لامپ نوع دوم بهتر است زیرا دارای میانگین طول عمر بیشتر و ضریب تغییر کمتری است.
توجه کنید در مثال بالا انحراف استاندارد نوع اول بخاطر وابستگی به واحد اندازه گیری از نوع دوم کمتر است در صورتی که پس از محاسبهی ضریب تغییر مشخص شد که میزان پراکندگی دادههای نوع اول بیشتر است.