با استفاده از قضیه حد مرکزی میتوان یک توزیع uniform را به یک توزیع normal تبدیل کرد.
در ابتدا مفاهیم ابتدایی را شرح میدهیم.توزیع Normal یا توزیع نرمالچ
توزیع نرمال یا گوسی مهمترین توزیع پیوسته در آمار و احتمال توزیع نرمال است. نموار این توزیع همانطور که در شکل مشاهده میکنید کاملا نسبت به یک حد متوسط متقارن است و به این منحنی که مانند زنگوله است منحنی نرمال میگوییم.
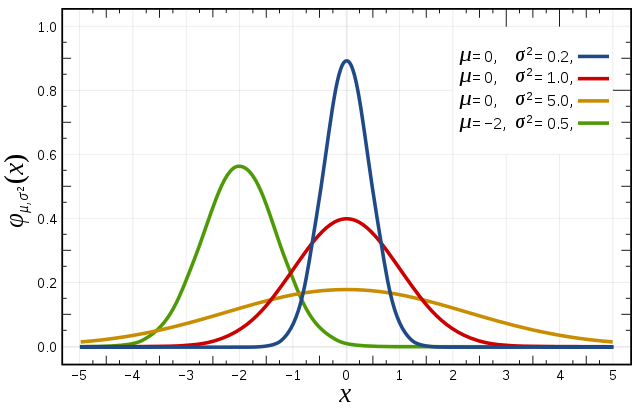
اغلب متغیرهای تصادفی پیوسته در طبیعت و صنعت دارای نموداری مانند نمودار منحنی نرمال هستند برای مثال اندازه قد افراد، میزان فشار خون افراد، میزان فروش یک رستوران و ... که بصورت کلی بیانگر این است که احتمال رخ دادن متغیری نزدیک به میانگین خیلی زیاد است و هرچه از آن دورتر میشویم احتمال رخ داد آن کمتر است. برای مثال در رابطه با قد افراد که توزیعی نرمال دارد میتوان به این نتیجه رسید احتمال اینکه قد یک نفر را که بصورت تصادفی انتخاب میکنیم نزدیک به میانگین قد تمام افراد جامعه باشد بیشتر از حالات دیگر است.
توزیع uniform یا یکنواخت
ساده ترین توزیع احتمال توزیع uniform یا یکنواخت است که در آن احتمال رخ داد مقادیر مختلف متغیر تصادفی X بعخرابر است.
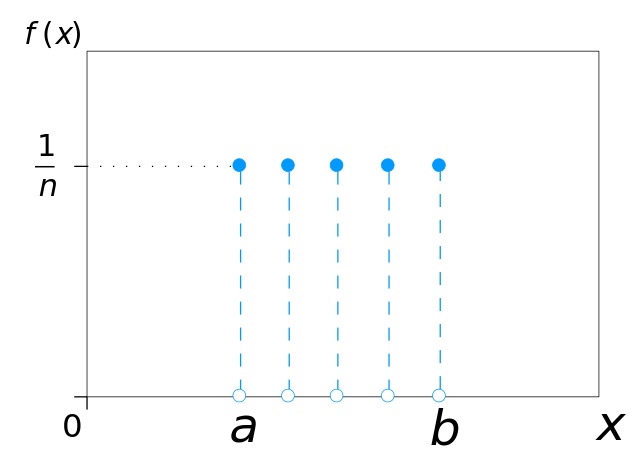
برای مثال فرض کنید بک صفحه هدف زنی را به ۱۵ قسمت مساوی تقسیم کردیم که احتمال برخورد تیر به هر قسمت برابر قسمت دیگر است. در این مثال متغیر تصادفی X که احتمال برخورد تیر به قطعههای بین ۱ تا ۱۵ میباشد شامل توزیع یکنواخت است. در مثال ما a برابر 1 و b برابر 15 و احتمال رخ داد هر یک از این مقادیر است.
قضیه حد مرکزی یا
Central Limit Theorem
بیان میکند که
مجموع تعدادی متغیر تصادفی مستقل، که هر یک میانگین و واریانس به خوبی تعریف شده دارند، بهطور تقریبی دارای توزیع نرمال خواهد بود. هرچه تعداد این متغیرهای مستقل افزایش یابد، این تقریب بهتر میشود.
تبدیل توزیع یکنواخت یا unifrom به نرمال یا normal در پایتون
ابتدا با استفاده از تابع random در پایتون که توزیعی نرمال دارد یک مجموعه از اعداد تصادفی با توزیع نرمال با تابع زیر تولید میکنیم.
def uniform_samples(n=10000):
samples=[]
for i in range (0, n):
samples.append(random.random())
return samples;هیستوگرام مجموعه بدست آمده با استفاده از تابع random که توزیع یکنواخت دارد بصورت زیر است.
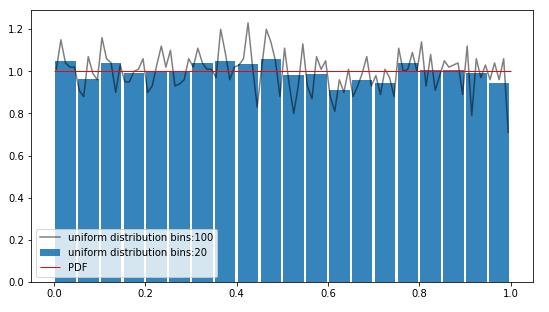
حال میخواهیم با استفاده از مجموعه بالا که یک توزیع یکنواخت دارد و قضیه حد مرکزی به یک مجموعه دیگری از اعداد با توزیع نرمال برسیم. برای تولید هر عدد در مجموعهی جدید کافیست به تعداد n که یک عدد بالایی مثل ۱۰۰۰۰۰ است نمونه از مجموعه اعداد دارای توزیع یکنواخت را با هم جمع کنیم و برای ایجاد عدد بعدی در این مجموعه جدید با توزیع نرمال n نمونهی مستقل دیگر از مجموعه قبلی با توزیع یکنواخت را با هم جمع کنیم تا در نهایت به یک مجموعه جدید از اعداد برسیم که با تقریب خوبی دارای توزیع نرمال است.
برای تولید هر نمونه جدید با استفاده از متد زیر هر بار n عدد جدید با توزیع یکنواخت یا uniform ایجاد کرده و با هم جمع میکنیم.
def u_samples_sum(n=10000):
total=0
for i in range (0, n):
total+=random.random()
return total; با استفاده از متد زیر
10000 نمونه جدید برای مجموعه جدید که توزیع نرمال دارد با 10000 بار فراخوانی متد بالا ایجاد میکنیم.
def get_normal_samples(n=10000):
samples=[]
total=0
for i in range (0, n):
uniform_sample_total = u_samples_sum()
samples.append(uniform_sample_total)
total+=uniform_sample_total
return samples,total; 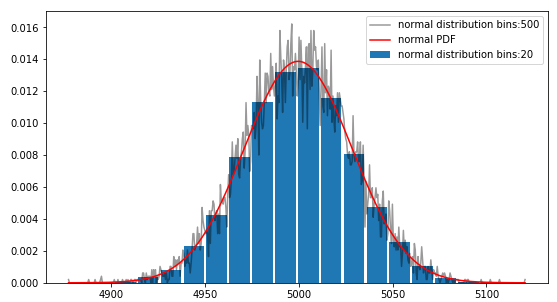
تمام کدهای این قسمت در
این لینک uniform_to_normal_distribution
در دسترس است.